Vergences and fractals
Field geologists have long known that the style and relationships of structures seen in a hand specimen, outcrop or drill core can mimic the style and relationships of much larger structures that formed during the same deformation but occur at the scale of a geological map or section. Since very large structures can seldom be directly observed, recognising these relationships has immense practical value when making a geological map or interpreting a drill section. The techniques are today generally known as the use of vergences and fractal (scale-invariance) relationships. Vergence and fractal relationships are two separate but related things which will be defined in the sections blow and an outline given of their application in practical field geology.
The idea of vergences was first enunciated in 1894[1] by the US Geological Survey Geologist Raphael Pumpelly[2]. According to Pumpelly:
The axes and axial surfaces of minor folds of an area are congruent with those of the major fold structures of the same phase of deformation.
This idea became known to several generations of geologists as Pumpelly’s Rule. Although strictly only a theory of fold and axial surface vergences, the Rule came to be associated with the idea that the general style of all minor structures was likely to mirror that of the major structures with which they were associated. With the invention of Chaos Theory in the 1970s and 1980s this latter aspect of Pumpelly’s Rule was recognised as a particular example of scale-invariance – a characteristic of objects that form through the operation of non-linear physical laws (i.e. – all naturally formed objects). Using the new mathematical language, geologists have taken to calling these relationships fractal (a better because more self-explanatory term is “scale-invariance”). Few geologists today have heard of Pumpelly’s Rule: this is a great pity, for this is one area where geologists anticipated mathematicians by almost 100 years, and Pumpelly was one of the greats of 19th century North American geologists. Here he is, in all his hirsute late Victorian glory:
Raphael Pumpelly (1832-1923). Eponymously famous for his Rule and the mineral Pumpellyite.
Vergences
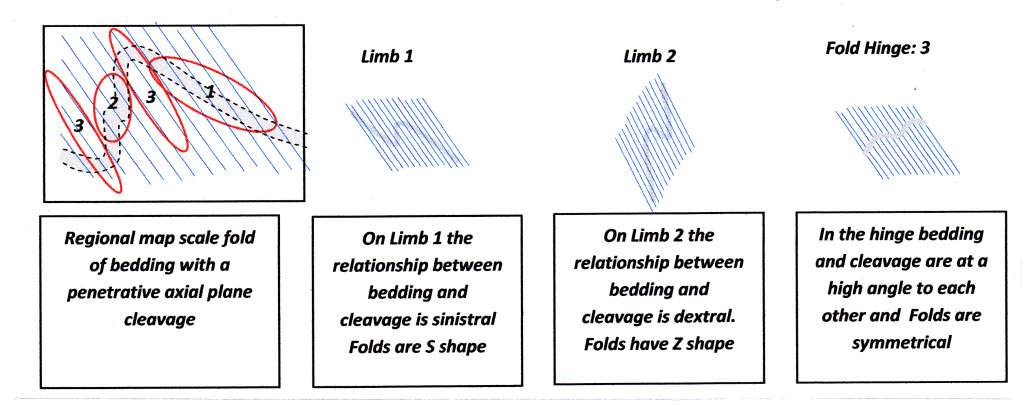
An axial-plane cleavage is a penetrative planar surface which (to a first level of approximation) bisects the angle between the two limbs of folded beds. The line of intersection of any cleavage plane with any one of the folded beds is approximately parallel to the axes of all major and minor folds that are associated with that deformation. On the illustration below, a folded bed is shown in grey and the cleavage as fine blue lines.
In the hinge area of the folds (the red-circled areas labelled 3 on the map), cleavage lies at a high angle to the beds; any minor second-order folds in the hinge area are symmetrical – that is, their 2-D profile shape has an “M” or “W” shape. In the hinge region, bedding/cleavage relationship and fold shapes are symmetrical. To the structural geologist, bedding and cleavage has a neutral vergence.
Examples of vergence relationships across a major fold
On the figure above, observe how the cleavage on Limb 1 of the large mapped fold lies at a much lower angle to the bedding than it does in the hinge. Compared to the relationships seen in the hinge, the cleavage on this limb is rotated to the left, in an anti-clockwise direction. Since in Latin the word for left is “sinister[3]” , this bedding/cleavage relationship is known as sinistral and described as having a sinistral vergence. Any minor second-order folds on this limb (parasitic folds) are asymmetric and also show an anti-clockwise or left-rotation sense of movement. Folds with this profile shape are known as sinistral folds. Such folds have a “S” shape so are also called S-folds.
On Limb 2 of the major fold, the cleavage also lies at a relatively-low angle to the bedding, but in this case the sense of rotation is clockwise or to the right. Latin for right is “dexter”, so such bedding/cleavage relationships are said to have dextral vergence. Associated folds have a “Z” shape in profile and are known as dextral folds or Z-folds.
Fold hinges are much less likely to be exposed at surface than fold limbs - there are good reasons for this as explained in the footnote below -[4]. However, by carefully observing and recording vergences on the exposures of the limbs, the opposed patterns of sinistral and dextral vergences across the mapped area enable the position of major unobserved fold hinges to be determined. In addition, measuring the plunge of minor folds and bedding/cleavage intersections will give an indication of the plunge of the major structure. The style of minor folds in outcrop will also give an indication of the style of the larger fold with which they are associated. This is an example of a fractal relationship rather than vergence, and will be described below in a separate section.
It is important to note that the sense of vergence given by the asymmetry of fold shape bedding/cleavage is, by convention, determined on the view the structure from above – i.e. a view looking down the fold axis or down the line of intersection of the bedding and cleavage. Since this is the way that geologists normally view an outcrop, the convention usually creates few problems. However care needs to be taken when making a geological map of an underground mine level where most available exposure is on the roof (called backs) of the mine opening. A dextral or Z-shape fold seen on the backs (necessarily looking up-plunge) needs to be shown on a map of the mine level as its mirror image - a sinistral or S-shaped fold: maps always show the view from above (another convention).
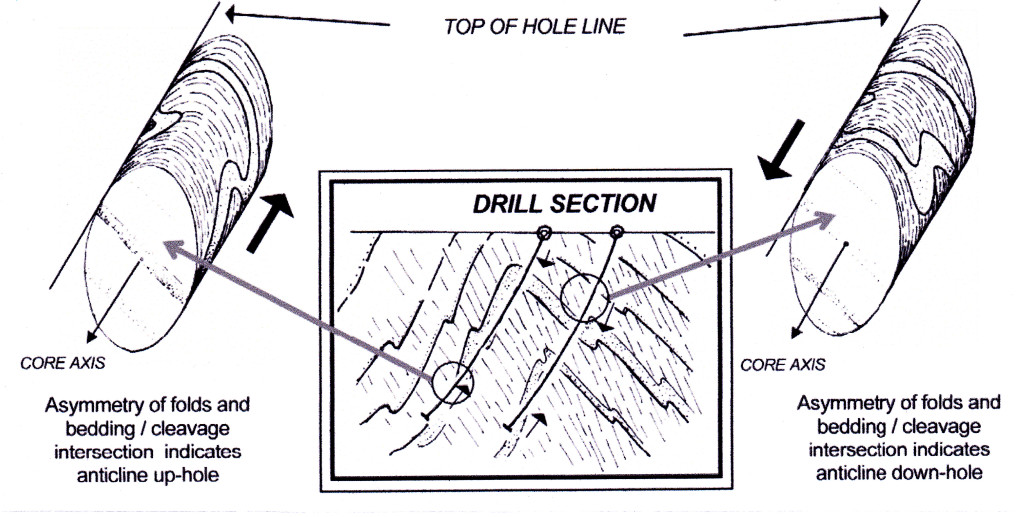
Vergences can be used to great effect when logging drill core, as illustrated in the figure below. If the core is oriented, the vergences of minor folds and bedding/cleavage can be interpreted in exactly the same way as vergences seen in outcrop. Vergence information is used to determine a vector pointing up or down the hole towards the position of the hinge of the major anticline or syncline in that hole. On the trace of the hole on a drill section, the vergence observations from the core (the vectors) can be shown as small arrows beside the hole trace that point up or down the hole. Such arrows greatly aid interpretation of the section.
In the illustration below, the vergence arrows plotted on the drill section point have been drawn to point towards the major anticlinal axis in the hole. Some structural geologists like to use arrows that point towards the syncline axis. This is because, when logging sedimentary rocks, a direction of younging – either up the hole or down the hole – can often be determined from sedimentary structure. If arrows are then plotted on the section to record younging direction, they will also point to towards the synclinal axis [5]. By combining arrows derived from vergence observations that point to the syncline, with younging direction arrows that provide the same information, there is a synergy from two different sources of knowledge that greatly aids interpretation. Needless to say, different kinds or colours of arrow are used on the plot to distinguish the two differently-derived vectors.
How vergence observations from oriented drill core can be used to help determine the position major fold axes on the drill section.
If the core is not oriented, vergence information is lost because there is no way of knowing whether the view of the structure is down-plunge or up-plunge since the view of any structure will change as the core is rotated. However, even in non-oriented core, it is possible to distinguish fold limbs (with low bedding/cleavage angles) from fold hinges (high bedding/cleavage angles) and this is valuable information to help in locating major unseen structure in the core.
Fractals or Scale Invariance
Scale invariance refers to the way that structures resulting from a single tectonic event exhibit similar styles of deformation at scales that can range from the microscopic to that of a regional map. Style refers to general aspects of the appearance of structures such as tightness, degree of irregularity, and asymmetry (but not the sense of asymmetry, that is not a fractal attribute) and so on. Since the characteristic essence of the shape of any natural object, regardless of its size, can be expressed as a fractal dimension, scale invariance relationships have come to be called fractals by geologists. A fractal dimension is a dimension between 1 and 2 if dealing with lines on a plane figure such as a map or section, and between 2 and 3 if dealing with a solid object. (I have attempted a definition of fractal dimension in footnote 6, below, but the subject is complex and really requires a whole post of its own see Link).
The word fractal has today become poplar amongst geologists, and has superseded the term Pumpelly’s Rule (which has priority but is a bit of a mouthful) and scale-invariance (which is a more accurate term and self-explanatory); perhaps this is because “fractal” is a short and easily-remembered word which trips off the tongue and sounds “sciency” and modern - and few people know what the word actually means.[6]. I fear the profession is stuck with fractal.
examples of fractal relationships at various geologically-realistic scales from regional map to thin section, are shown in the illustration below.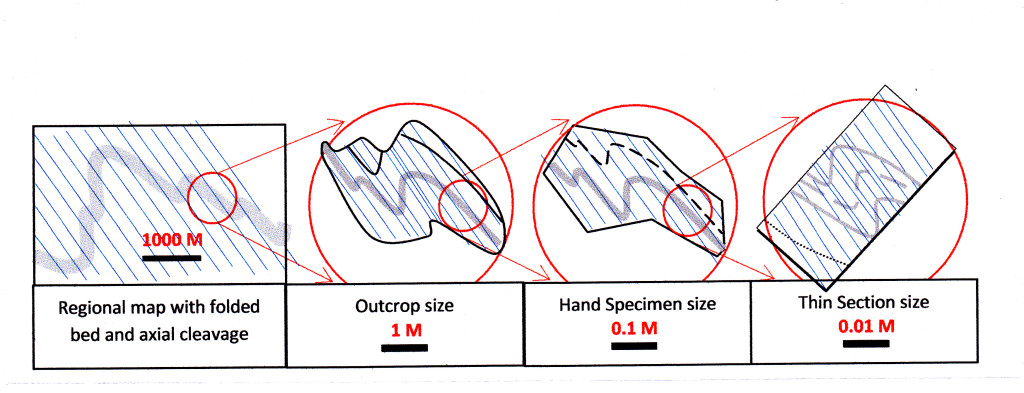
Examples of scale-invariate, or fractal, relationships across a range of geological scales
If I were to parody Jonathon Swift, I might say:
So, Geologists observe, a fold,
Hath smaller folds that on limbs prey,
And these have smaller yet to parasite ‘em,
And so proceed ad infinitum.
Of course, in Nature, self-similarity is never literally found through an infinite range of scales.
[1] Pumpelly R, Wolff JE & Dale TN: 1894. The Geology of the Green Mountains, USGS Memoir 23, 157p.
[2] After whom the zeolite mineral pumpellyite was named.
[3] Our present day dictionary meaning for the word “sinister” reflects a former prejudice against the left-handed.
[4] The reason is obvious: the area of a hinge is usually small compared to its limbs and, because hinges have more intense cleavage development, they are more prone to weathering and less likely to be exposed at surface anyway.
[5] This is because sedimentary rocks young into synclines and get older into the cores of anticlines.
[6] The mathematician Benoit Mandelbrot (he of the famous Mandelbrot Set) realised in the 1970s that objects with complex shapes could not be usefully descibed by the then mutually-exclusive categories of one-dimensional, two-dimensional, three-dimensional etc.. A line (one-dimension), he reasoned, could be so complexly folded that it tended to fill space on a plane and so approach two-dimensions. The attributes of degree and type and style of folding of the line could be characterised as a unique dimension somewhere between 1 and 2: this would be a fraction of a dimension – a number such as, say, 1.32 or 1.87. Mandelbrot called this the fractal number. Similarly, a two-dimensional object (a sheet of paper, say) could be so folded that it would approach the solidity of a 3-D object. A sheet of paper scrunched into a ball will have a fractal number somewhere between 2 and 3. Any complex shape produced by a natural process has a characteristic fractal dimension. Mountains have a characteristic range of fractal dimensions. So do trees. An outcrop of granite has a different fractal shape from an outcrop of shale. A protein is linear chain of amino acids (1-D) that when folded, then re-folded, and triple folded results in a lumpy, infolded molecule with a fractal dimension not much less than 3. The trace of a rocky coastline on a map has a characteristic shape (fractal dimension) that is instantly recognisable whether it is a line on a million scale map of a continent, a ten thousand scale map of a rocky bay or a one-on-one-scale map of a rock pool. In each case details differ and an infinity of shapes are possible, but the fractal dimension of the line on the map is the same. (a rocky coastline has a fractal dimension of around 1.3. Slartibartfast used the slightly higher number of 1.52 when he designed the Norwegian fjords, for which he got an award). The key point is this: fractal dimension is independent of size. (Source of numbers quoted www.ems.gphys.unc.edu)