Stereonet solutions for non oriented drill core
Shawn Harvey of Saskatchewan sent me this email earlier this year:
Hello again Roger,
You previously helped me out with some alpha-beta stereonet solutions which worked great (thanks again!!). I am now looking into a slightly more complex stereonet issue. I have some semi-oriented core in which I have a “known” orientation of a foliation and want to use this plane to help calculate the orientation of a fault relative to this foliation. I have made the alpha measurement for the fault and the beta measurement relative to the bottom of ellipse mark for the foliation (i.e. Beta angle between the foliation reference line and the bottom of ellipse for the fault plane). Ideally I would use a core frame but the facility is metal rich and compass accuracy is an issue and it is -30 degrees Celsius outside; as such, I was hoping to use the stereonet to convert the internal angle relationships to geographic coordinates. I could also use Geocalculator but I would really like to understand the derivation of the results.
For the alpha-beta solution of planes I have used your 6 step process from your 2010 publication but I was hoping you could pass on how to modify the steps for the semi-oriented core calculations. Your assistance would be greatly appreciated.
thanks, shawn
Good morning Shawn,
I appreciate your problems. –30 degrees sounds pretty tough. After a lifetime of working in Australia I find UK winter temps of –1 or –2 a trial. Where are you? Northern Canada?
Your other problem with the semi-oriented magnetic core is obviously susceptible to a stereonet solution, but I will have to think about it a bit. Maybe this weekend ? I will get back to you.
Best wishes, Roger
Statement of the problem
Non oriented core (i.e. no bottom of hole line on core). However, the drill hole has been surveyed and the azimuth and inclination of the core axis (CA) are known.
The core contains two structures: a foliation (labelled s) and a fault (labelled f).
The dip and dip direction of the foliation are known from other data.
The orientation of the fault is unknown.
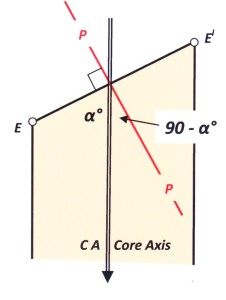
We have the following measurements on the fault: (1) its alpha angle (αf) and, (2) the angle measured around the core circumference in a clockwise direction between point E for the foliation (Es) and point E for the fault (Ef ). We will call this radial angle theta (ϴ). Note that the radial angle between Elsand Elf is also ϴ.
Using a stereonet, calculate the strike and dip of the fault.
A Worked example:
CA(Core Axis): 56° to 240°; s (foliation): 078/60 South; α (for fault): 45°; ϴ (as defined above): 25°
Es and Els : mark the ends of the long axis of the intersection ellipse of the foliation (s)
Ef and Elf: mark the ends of the long axis of the intersection ellipse of the fault (f)
Procedure
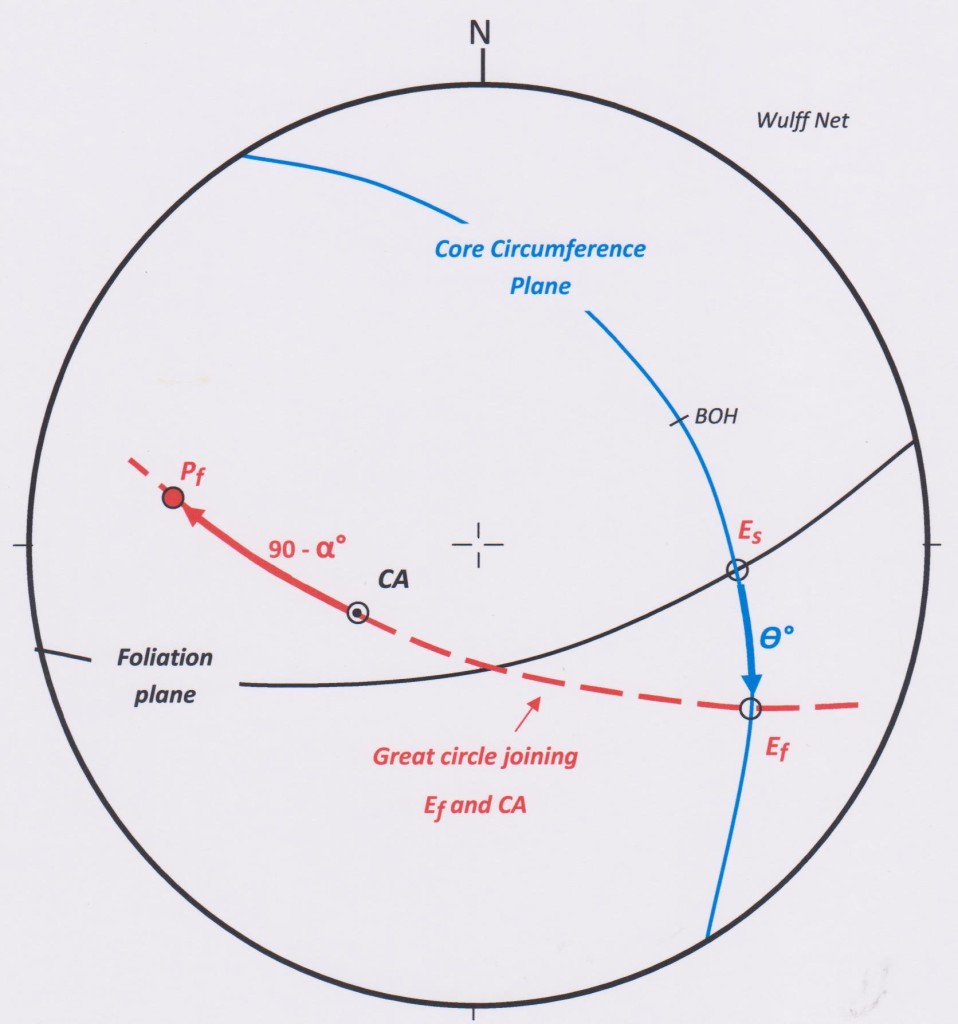
Stereonet solution to problem. The fault strikes 010 and dips 69 east
Step 1: On the stereonet plot the information that is known; i.e the Core Axis, the core circumference plane (the plane at right angles to the CA) and the trace of the foliation (s).
Step 2: The intersection of the foliation plane and the circumference plane is the plot of the long axis the intersection ellipse of the foliation. If this plots in the lower quadrant of the circumference plane (as in our example) then the point represents Es. If it plots in the upper quadrant then it represents Els (E primed).
Step 3: Along the circumference plane, in a clockwise direction from Es (or Els) , measure the angle theta (ϴ). This will plot either point Ef or Elf.
Step 4: By rotating the stereonet overlay, locate and plot the Great Circle that connects points CA and Ef (or Elf).
Step 5: Along this Great Circle, starting at point CA, measure the angle (90-α)f . If Ef has been plotted, measure the angle in the direction away from Ef (as in the worked example). If Elf has been plotted, measure 90-α in a direction towards Elf. This plots the pole to the fault plane (Pf)
Step 6: From the pole to the fault read off its strike and dip : in this example strike 010° dip 69° E
Longitudinal section of core in the plane of the Core Axis, and the long axis of the intersection ellipse of a cross-cutting plane.