A stereonet solution for alpha beta angles in oriented drill core

Using a stereonet to calculate strike and dip from alpha-beta angles in oriented drill core

The attitude of a surface in oriented drill core can be determined by the measuring two internal core angles known as alpha (α) and beta (β). These numbers are then normally entered into a software program which calculates the strike and dip of the surface[1].  There is a simple and quick stereonet procedure which produces the same results.

How to use a stereonet to convert alpha and beta angles in to strike and dip is the subject of this post. 

Oriented drill core is core which meets three criteria:

1. A down-hole survey has established the azimuth and inclination of the core axis  along its length.
2. A core orientation survey has established the intersection of the original gravity vector  with the core surface. This is usually shown as a line, called the Bottom of Hole Line, marked along the original bottom surface of the core.
3. The down direction of the core is marked by an arrow placed on each piece of core. For holes angled below the horizontal (that is, all surface holes) these arrows will point away from the hole collar towards the hole termination.  For holes angled above the horizontal (some underground holes) the arrows on the core will point towards the hole collar and way from the hole termination.

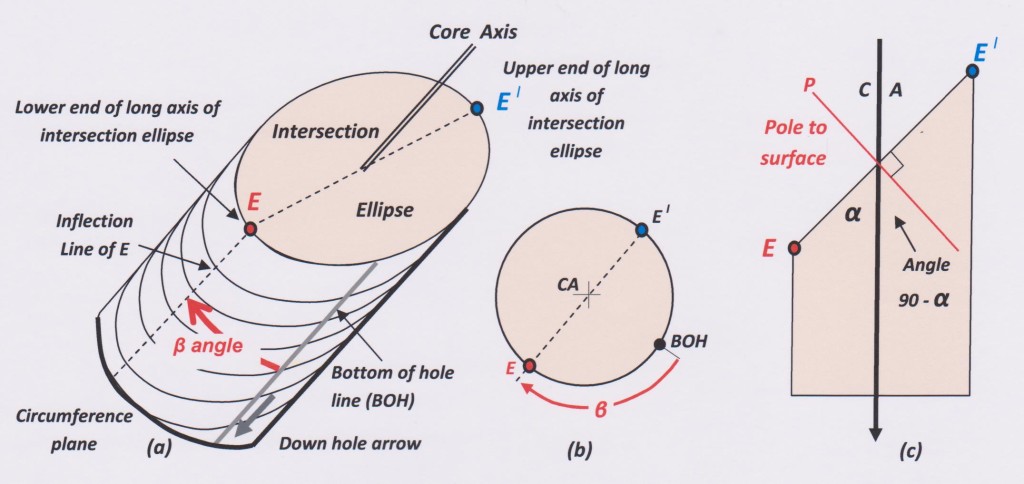
Figure 1: The geometry of a planar structure in drill core. (a) is a perspective view of a piece of drill core containing a penetrative planar structure (bedding or cleavage) along which the top of the core has broken. (b) is a view looking down the core axis. (c) is a longitudinal section through the core containing the core axis, the long axis of the intersection ellipse of the planar structure and the pole to that structure.

The internal reference lines and planes in oriented core

These are:

 1. The Core Axis (i.e. the imaginary line along the centre of the core), labelled CA.

2.  The plane at right angles to the core axis, known as the circumference plane (by some, the propeller plane).

3. The bottom of the hole line – labelled BOH.

4. The long axis of the intersection ellipse of the planar structure. This line requires some further explanation:

The trace of any planar rock structure on the surface of cylindrical drill core defines an ellipse, known as the intersection ellipse.  The long axis of the ellipse is marked on the core surface by points of maximum curvature on the trace of the plane. These are called inflection points.There are two inflection points marking the opposite ends of the long ellipse axis.

The inflection point that makes an acute angle with the down direction core axis is known as point E. The inflection point that makes an obtuse angle with the down direction core axis is known as point E^l ( pronounced E primed).

Note the two special cases:

1. Where a hole is drilled at right angles to the planar structure, then the trace on the core surface is a circle and no ellipse long axis is definable.
2. Where a hole is drilled parallel to a structure, the trace of the structure trends along the along the length of the core and no inflection points can be defined – at any rate, for as long as this particular geometry holds good (which in real rocks is seldom more than a meter or so). 

The orientation of a planar structure in core is defined by two angles (figure 1)

1. The acute angle between the core axis and the long axis (E-E^l) of the intersection ellipse. This angle is known by the Greek letter alpha – whose symbol is: α   The alpha angle can be measured in any core, irrespective of whether the core is oriented or even whether the hole is surveyed. 
2. The radial angle between the BOH line and the point E.  This angle is measured from BOH around the core circumference in a clockwise direction.  Note that ”clockwise” refers to a view looking down the core (i.e. in the direction of the arrow marked on the core).  The angle is known by the Greek letter beta – whose symbol is: β

Now for the stereonet procedure…

Step 1:  Plotting the core reference lines and planes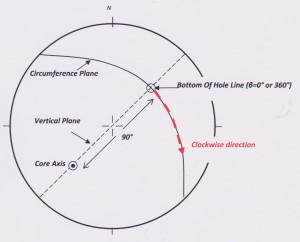

Figure 2: Stereonet plot of reference lines and planes for a hole drilled at – 45° to 225° azimuth or + 45 to 045 (click for larger image).

On a stereonet lines plot as points and planes plot as great circles (i.e. planes which pass through the centre of the sphere). The azimuth and inclination of the core axis (at the depth of the measured structure) enables it to be plotted as a point on the net. The core circumference plane is a great circle at 90° to the plot of the core axis. A vertical plane is a straight line passing through the centre of the net. The circumference of the stereonet is the horizontal plane. The BOH line is the point where the vertical plane passing through the core axis intersects the lower half of core circumference plane.

A plane can also be shown by plotting the line that is normal to the plane (this point is known as the pole to the plane). The core axis is the pole to its circumference plane. 

Remember that a stereo net is a projection of the lower half of a sphere and the centre of the net represents the down direction of the vertical (the line pointing to the centre of the earth: the gravity vector).   To a stereonet, a drill hole is a line oriented in space.  The direction in which the hole was drilled is immaterial.  This means that an underground hole that is inclined at +45 degrees above the horizontal towards azimuth 045 ° will be plotted on the net as a line at -°45 (below the horizontal) to 225° (the reciprocal of the azimuth).

 Step 2: Plotting the beta (β ) angle.

This is the step where most care needs to be exercised.

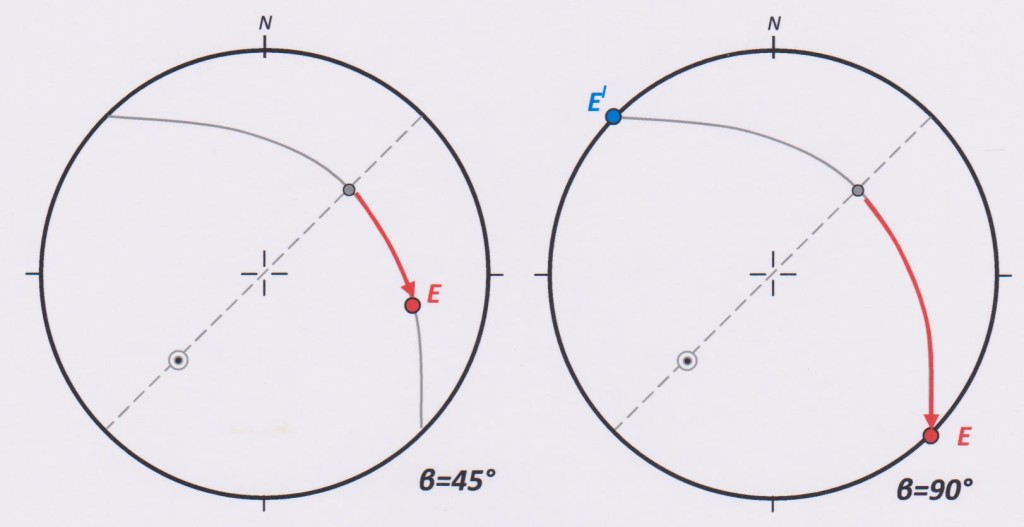
The beta angle defines the position of the long axis of the intersection ellipse on the net. This  line ( E –E^l ) is represented by a point on the net.  The angle is measured in a clockwise direction along the trace of the circumference plane, starting at point BOH.  For all beta values between 0° and 90°, point E lies on the net (see left diagram of figure 3).  When beta is 90 ° (figure 3, right) point E lies on the circumference of the net, indicating a horizontal line. The opposite end of that line is point E^l , which now lies on the net circumference at the diametrically opposite side of the net from point E.

Figure 3: Plotting the beta angle for the range β=0° to β=90°

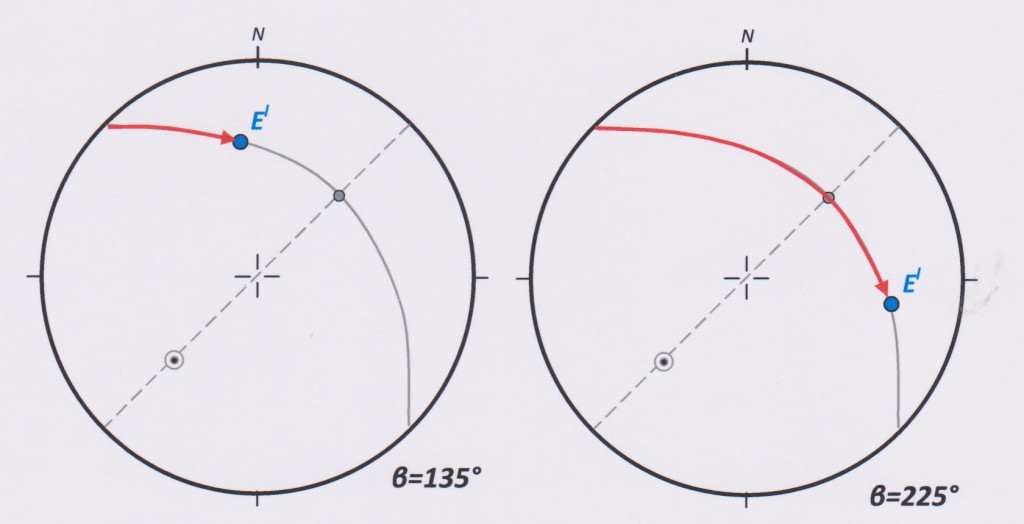
For all beta angles between 90° and 270° , the E end of the long axis of the intersection ellipse is rotated out of the net projection and cannot be shown (it may help to think of E as now pointing “up in the air” out of the plane of the page). However, for this range of beta angles, the opposite end of the axis, E^l , is now rotated on to the net and its position can be plotted by continuing to measure beta around the circumference plane.  The measurement is now made from the point where the left edge (“left” when looking in the direction of dip) of the core circumference plane meets the net circumference. This point is β = 90° (figure 4).

Figure 4: Plotting the beta angle for the range 90° to 270°

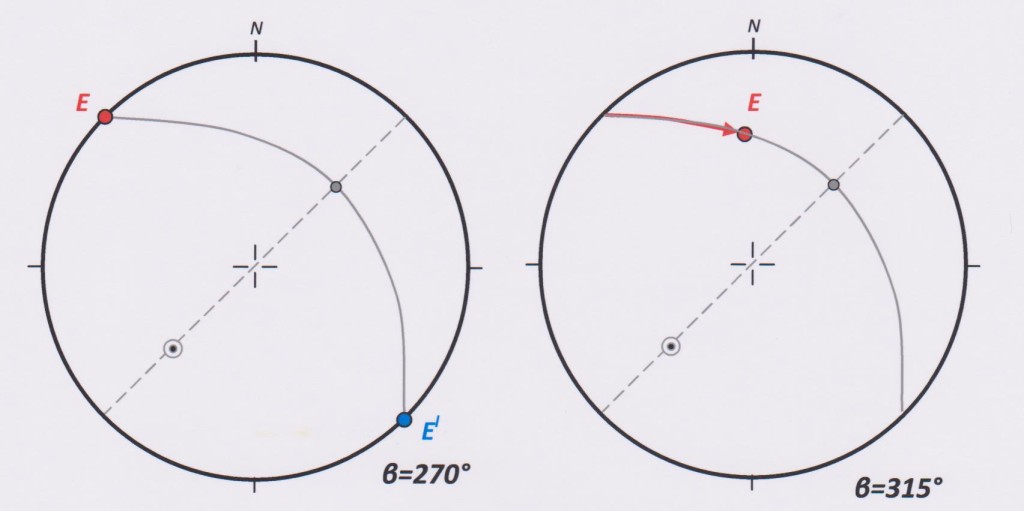
When the beta angle is exactly 270°, the line E – E^l is again horizontal and its two end points lie at diametrically opposite locations on the circumference of the net as shown in figure 5, left. In this case, point E is on the left, and E^l is on the right (compare to the plot of β=90° on figure 3, right diagram).

For all beta angles in the range 270° to 360°, point E will plot once again on the net (right diagram of figure 5). The left intersection of the circumference plane with the net circumference represents 270°.

Figure 5: Plotting the beta angle for the range 270° to 360°.

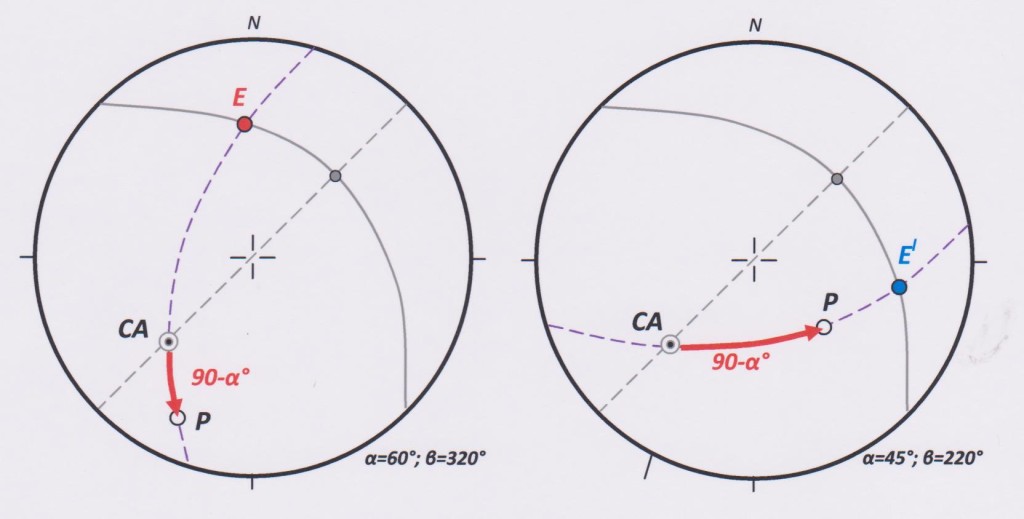
 Step 3: Plotting the Alpha angle

By rotating the overlay, locate the great circle which contains the points CA and E (or E^l).  There is only ones such great circle. This is the trace of the longitudinal core section shown at (c) on figure 1.

On figure 6, the great circle has been drawn as a purple dashed line. Along this line, starting at the point CA, measure the angle 90-α °.  If point E has been plotted on the net, the angle 90-α° is measured in a direction away from point E (as in figure 6, left).  If point E^l is plotted on the net, the 90-α° angle is measured in a direction towards E^l (figure 6, right).  The logic of this step should be obvious from figure 1(c). The measurement locates point P - the pole, or normal, to the planar rock structure being measured.

Once the pole to the plane has been plotted, the net scales can be used to read off the its dip and dip direction, strike and dip, or apparent dip on drill section, as required.

Figure 6: Plotting the alpha angle and locating the Pole

Speed and Accuracy

On a standard 15 cm stereonet, the thickness of a pencil line or point is 1-5 degrees, depending on where the line is on the net. As a result, most stereonet measurement can be considered, as a rule of thumb, to be within one or two degrees of the correct value. That is to say, a stereonet measurement of 45° could be anywhere between 43° and 47°.  By contrast, mathematical manipulation of spatial data would give exact numbers, to a fraction of a degree if required, and limited only by the accuracy of the input numbers. But calculating a figure with this sort of accuracy would be both misleading and spurious. Plus or minus 2 degrees is an entirely appropriate and acceptable range of accuracy for geological measurements. In fact, most geologists would consider themselves favoured if their result is within 2° of the notional “correct” answer. This is because “planar” rock structures are seldom perfectly planar or constant in orientation over distances of more than a few tens of centimetres. In addition to this, orientation lines marked on core are generally considered acceptable if the match of the BOH orientation line from run to run, or from core piece to core piece, is less than +/- 5°.  Finally, measurements of alpha and beta angles (and especially of beta angles) taken by geologists on core typically have similar levels of accuracy. Fortunately, these various sources of error are not cumulative – that is what a +/- designation means.

The long verbal description and many figures that I have had to use in describing the stereonet reduction of internal core angles probably has given the reader the impression that this is a long and complex process. So that the logic of the solution and the plotting techniques can be understood I have shown all the construction lines. However, after a little practise, it will be found that most of these lines can be omitted. Almost everything can be done by eye using the pre-printed net scales, and just two points need to be plotted on the net overlay. Here is how it is done:

1. Plot the core axis and BOH points on the net overlay with permanent inked marks.  A single plot of these points will usually be good for a large number of measurements taken on core with that axial orientation (deviations in the hole azimuth and inclination of less than 2 degrees can be safely ignored).

2. Rotate the BOH point on to a principal net diameter. Using the degree divisions of the net, use angle beta to locate point E (or E^l) and mark this onto the overlay with a pencil mark.

3. Rotate the overlay again so as to bring points CA and E (or E^l ) on to a great circle, then, with the overlay in this position, measure the angle 90 minus alpha to locate the pole to the plane. Mark this point on to the overlay with a pencil.

4. Rotate the pole to the plane on to a principal net diameter:  read off the dip and dip direction of the plane from the scales of the net.

Now erase the two pencil marks to be ready ready for the next calculation.

Total time – 20 seconds.

Try beating that, from cold, with a computer.

---